Coatings
Hard coatings on metal and ceramic substrates have drawn increasing attention to materials scientists due to their attractive functions in mechanical, thermal and chemical protection. The Young’s modulus is an important parameter for a safe design and application of the different coating/substrate systems.
Over the years, many methods have been developed to investigate the properties of the coatings. As the indentation test is the most popular one, it only measures the local properties which can deviate from the overall characteristics in case of coatings with high porosity or the presence of cracks. As an indirect approach, the impulse excitation technique (IET) is used to analyze the coating properties.

Application note: Young’s modulus analysis of coatings
S. Paul applied several techniques to characterize the stiffness of plasma sprayed thermal barrier coatings (TBC) and the effects of the sintering process on these properties. The sintering-induced microcrack healing and improved inter-splat bonding can cause shrinkage and stiffening of the top coating. The samples were made of yttria-stabilised zirconia (YSZ) onto steel substrates. The coating thickness ranges from 0.65 up to 1.4 mm. The IET was used to measure the Young’s modulus of the attached and detached coatings before and after the heat treatments in air at 1200 °C and 1400 °C.
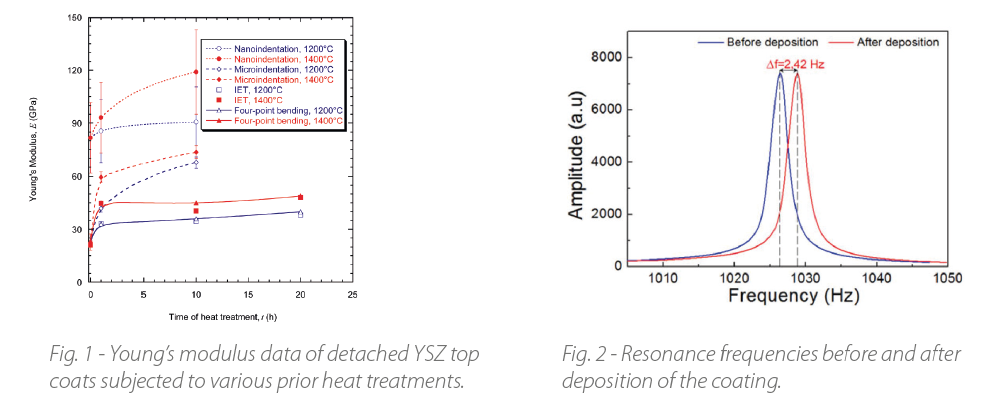
The Young’s modulus of the coating is calculated based on the Euler-Bernoulli beam theory taking into account a shift of the neutral axis due to the coating deposition. This resulted in a Young’s modulus of 22 GPa for the attached TBC coating. To obtain a global in-plane stiffness of the TBC, measurements were performed on free-standing coatings. The Young’s modulus of the detached coating was 22 ± 3 GPa which was in agreement with the four-point bending test. In Fig. 1, the effect of the heat treatment on the stiffness of plasma sprayed YSZ can be seen as a significant increase in Young’s modulus. A large scatter in the data is shown dependent on the used analysis technique. When using the indentation technique, only the elastic behavior of some splats can be determined because of a minimal measuring volume, while IET can be used to give the global Young’s modulus of the coating both when attached to the substrate and detached from it.
The IET can also be used to analyze thin films. M.F. Slim et al. deposited an aluminum film (thickness of 7 um) on a stainless substrate with a thickness of 1 mm by DC magnetron sputtering. The resonance frequency was measured before and after deposition and the results are shown in Fig. 2. These two frequencies are used in the formula’s to calculate the Young’s modulus of the substrate and subsequent of the thin film.
They investigated different models available in the literature to calculate the Young’s modulus of the coating and developed a numerical finite element model to estimate the systematic errors by the models. This resulted in the model that takes into account the shift of the neutral axis to be the most complete one with a perfect agreement with the numerical values obtained by the simulation. They suggest this model- where the new ISO 20343 standard is based on – to determine the Young’s modulus of a coating for any thickness, Young’s modulus and density ratios. They concluded also that the standard uncertainty on the substrate Young’s modulus comes mainly from the uncertainty on its density and on its thickness. For the coating itself, the main sources of uncertainty are the density and the thickness of the coating and the frequency before and after coating.
Based on these results, it is clear that the impulse excitation technique can be used as a tool to determine the global Young’s modulus of uniform coatings with an accurate known thickness. Based on the ISO 20343 standard, analyses are possible at room temperature and continuously at elevated temperatures with the dedicated IMCE RFDA room temperature systems and furnaces.
References
- S. Paul, Stiffness of plasma sprayed thermal barrier coatings, Coatings, 7 (2017) 68.
- M.F. Slim et al., On the determination of Young’s modulus of thin films with impulse excitation technique, Journal of Materials Research, 32 (2017) 497-511.
